مثلث قائم الزاویه: تفاوت میان نسخهها
Mohammadi3 (بحث | مشارکتها) جز (Mohammadi3 صفحهٔ مثلث قایم الزاویه را به مثلث قائم الزاویه منتقل کرد) |
Mohammadi3 (بحث | مشارکتها) بدون خلاصۀ ویرایش |
||
| خط ۴: | خط ۴: | ||
[[File:38137300.jpg|thumb|مُثَلّث قائمالزاويه]] | [[File:38137300.jpg|thumb|مُثَلّث قائمالزاويه]] | ||
مثلثی با یک زاویۀ قائمه(۹۰ درجه). این مثلث، مثلث مرجع برای تعریف نسبتهای مثلثاتی<ref>trigonometrical ratios</ref>، مانند سینوس<ref>sine </ref>، کسینوس<ref>cosine </ref>، و تانژانت<ref>tangent </ref>، است و قضیۀ فیثاغورس<ref>Pythagoras’ theorem</ref> در آن برقرار است. بلندترین ضلع مثلث قائمالزاویه را وتر<ref>hypotenuse </ref> مینامند. مساحت این مثلث نصف حاصلضرب طولهای دو ضلع کوچکتر است. مثلثی که یک ضلع آن قطر<ref>diameter </ref> یک دایره و رأس روبهروی آن ضلع روی محیط دایره باشد، قائمالزاویه است. این مضمونِ قضیهای بنیادی در هندسه است که کشف آن را به تالس<ref>Thales</ref>، ریاضیدان یونانی (ح ۵۸۰پم)، نسبت میدهند. | مثلثی با یک زاویۀ قائمه (۹۰ درجه). این مثلث، مثلث مرجع برای تعریف نسبتهای مثلثاتی<ref>trigonometrical ratios</ref>، مانند سینوس<ref>sine </ref>، کسینوس<ref>cosine </ref>، و تانژانت<ref>tangent </ref>، است و قضیۀ فیثاغورس<ref>Pythagoras’ theorem</ref> در آن برقرار است. بلندترین ضلع مثلث قائمالزاویه را وتر<ref>hypotenuse </ref> مینامند. مساحت این مثلث نصف حاصلضرب طولهای دو ضلع کوچکتر است. مثلثی که یک ضلع آن قطر<ref>diameter </ref> یک دایره و رأس روبهروی آن ضلع روی محیط دایره باشد، قائمالزاویه است. این مضمونِ قضیهای بنیادی در هندسه است که کشف آن را به تالس<ref>Thales</ref>، ریاضیدان یونانی (ح ۵۸۰پم)، نسبت میدهند. | ||
<br/> <!--38137300--> | <br/> <!--38137300--> | ||
نسخهٔ کنونی تا ۱۸ آوریل ۲۰۲۵، ساعت ۲۲:۲۹
مُثَلّث قائمالزاویه (right-angled triangle)
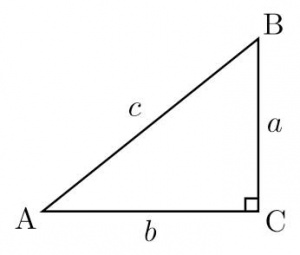
مثلثی با یک زاویۀ قائمه (۹۰ درجه). این مثلث، مثلث مرجع برای تعریف نسبتهای مثلثاتی[۱]، مانند سینوس[۲]، کسینوس[۳]، و تانژانت[۴]، است و قضیۀ فیثاغورس[۵] در آن برقرار است. بلندترین ضلع مثلث قائمالزاویه را وتر[۶] مینامند. مساحت این مثلث نصف حاصلضرب طولهای دو ضلع کوچکتر است. مثلثی که یک ضلع آن قطر[۷] یک دایره و رأس روبهروی آن ضلع روی محیط دایره باشد، قائمالزاویه است. این مضمونِ قضیهای بنیادی در هندسه است که کشف آن را به تالس[۸]، ریاضیدان یونانی (ح ۵۸۰پم)، نسبت میدهند.
