حساب
حساب (arithmetic)

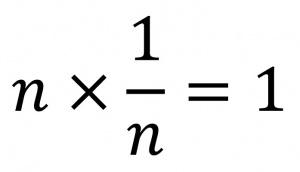
شاخهای از ریاضیات، برای بررسی اعداد، بهویژه اعداد صحیح مثبت[۱]، و خصوصیات آنها. چهار عمل اصلی حساب عبارتاند از جمع[۲]، تفریق[۳]، ضرب[۴]، و تقسیم[۵]. بهتوانرساندن[۶]، ریشهگرفتن[۷]، درصدگرفتن[۸]، و تشکیل کسر[۹] و نسبت[۱۰] از این عملهای اصلی مشتق میشوند. اشکالی از حساب ساده در دورانهای ماقبل تاریخ بهکار میرفتهاست. در چین، مصر، بابِل[۱۱]، و کلاً در تمدنهای اولیه، حساب را برای مقاصد تجاری، محاسبۀ مالیات، و نجوم[۱۲] بهکار میبردند. در قرون وسطا، دانش حساب در هند و سپس در میان مسلمانان محفوظ ماند. ریاضیات اروپایی با رشد بازرگانی و اکتشافات جغرافیایی جانگرفت. ارقام هندی-عربی جانشین ارقام رومی شد و بهاینترتیب، محاسبه بر روی کاغذ، بهجای استفاده از چرتکه میسر شد. ویژگی اساسی دستگاه اعداد هندی ـ عربی وجود رقم صفر بود که امکان استفاده از دستگاه اعداد مبتنیبر ارزش مکانی را میسر میکرد. در دستگاه دهدهی[۱۳] یا اعشاری، ده رقم (۹،۸،۷،۶،۵،۴،۳،۲،۱،۰) بهکار میرود و گفته میشود این دستگاه در پایۀ دَه است. در عدد دهدهی، هر مکان ارزشی دارد که ده برابر ارزشِ مکان سمت راست آن است. به این مکان مرتبه هم میگویند. مثلاً در عدد ۲۳، رقم ۳ در مرتبۀ یکان و نشاندهندۀ ۳ تا ۱ است و رقم ۲ در مرتبۀ دهگان و نشاندهندۀ ۲ تا ۱۰. ولی بابِلیها از دستگاهی پیچیده در پایۀ شصت استفاده میکردند که بقایای استفاده از آن را امروز در تقسیم ساعت به ۶۰ دقیقه و نیز تقسیم درجۀ زاویه به ۶۰ دقیقه میبینیم. مایاها[۱۴] از دستگاهی در پایۀ بیست استفاده میکردند. در طول تاریخ، ابداعات بسیاری صورت گرفت تا عملیات حسابی آسانتر صورت گیرد، ازجمله ابداع جان نپر[۱۵]، ریاضیدان اسکاتلندی، که در ۱۶۱۴ لگاریتم[۱۶] را ابداع کرد. خطکش محاسبه[۱۷] در دهۀ ۱۶۲۰ اختراع شد. از آن زمان به بعد، اَشکال متعددی از حسابگرها، ماشینهای حساب مکانیکی و الکترونیکی، و رایانهها اختراع شدهاست. رایانههای جدید اساساً در پایۀ دو عمل میکنند، یعنی با استفاده از دستگاهی که فقط دو رقم (۰,۱) دارد و به دستگاه دودویی[۱۸] موسوم است. در عدد دودویی، هر مکان ارزشی دارد که دو برابر ارزش مکان سمت راست آن است. مثلاً عدد دودویی ۱۱۱ برابر با ۷ در دستگاه دهدهی، و عدد دودویی ۱۱۱۱ برابر با ۱۵ در دستگاه دهدهی است. از آنجا که اعمال عمدۀ تفریق، جمع، ضرب، و تقسیم را از لحاظ ریاضی میتوان به جمع تبدیل کرد، رایانههای دیجیتال (رقمی) محاسبات را با جمعکردن صورت میدهند، معمولاً از عددهای دودویی استفاده میکنند، و رقمهای ۰ و ۱ را با پالسهای روشن و خاموش جریان الکتریکی نشان میدهند. در حساب پیمانهای[۱۹]، که گاهی حساب ماندهای[۲۰] یا حساب ساعتی[۲۱]هم نامیده میشود، تعداد مشخصی از ارقام را براساس پیمانه بهکار میبرند. مثلاً در پیمانۀ ۴، مقادیری که هر عددی میتواند داشته باشد فقط ۲،۱،۰ یا ۳ است. در این دستگاه، ۷ بهصورت ۳، به پیمانۀ ۴، و ۳۵ نیز بههمین صورت نوشته میشود. توجه کنید که ۳، ماندۀ تقسیم ۷ یا ۳۵ بر ۴ است. این نوع از حساب را غالباً با دایره نمایش میدهند و با رویدادهایی سروکار دارد که در چرخههای منظم روی میدهند؛ ازجمله برای توصیف عملکرد موتورهای بنزینی، مولدهای برق، و نظایر اینها کاربرد دارد. مثلاً در پیمانۀ ۱۲، که حساب ساعت مبتنیبر آن است، پاسخ این پرسش که اگر اکنون ساعت ۱۰ باشد، ۵ ساعت دیگر چه ساعتی خواهد بود، چنین بیان میشود: ۳ = ۵+۱۰ قوانین حاکم بر جمع و ضرب اعداد در حساب معمولی عبارتاند از الف. قانون تعویضپذیری[۲۲] (جابهجایی)، یعنی میتوان ترتیب عوامل را در جمع و ضرب عوض کرد (← عمل تعویضپذیر) یا به زبان نمادین a+b=b+a و ab=ba. ب. قانون شرکتپذیری[۲۳] برای جمع سه عدد، به این معنا که خواه مجموع عددهای دوم و سوم را به اولی بیفزاییم، و خواه عدد سوم را با مجموع اولی و دومی جمع کنیم، حاصلجمع تفاوت نمیکند. این قانون در ضرب سه عدد نیز صادق است (← عمل شرکتپذیر) یا به زبان نمادین a+(b+c)=(a+b)+c و a(bc)=(ab)c. ج. قانون توزیعپذیریِ[۲۴] جمع نسبت به ضرب، یعنی برای ضربکردن مجموع دو عدد در عددی دیگر، میتوان هر یک از عوامل مجموع را در آن عدد ضرب و حاصلضربها را باهم جمع کرد (← عمل توزیعپذیر) یا به زبان نمادین a(b+c)=ab+ac. عنصر همانی[۲۵]یا خنثی برای جمع عدد صفر است، زیرا افزودن صفر به هر عدد هیچ تأثیری در حاصل ندارد، n=۰+n=n+۰ . عنصر همانی برای عمل ضرب عدد یک است، زیرا ضربکردن یک در هر عدد تغییری در آن عدد نمیدهد n = ۱ × n = n × ۱ قرینه، یا منفیِ هر عدد، مانند n، عددی است مانند n - بهطوریکه n + (-n) = ۰. عکس هر عدد مانند n، بهجز صفر، عددی است بهصورت (فرمول ۱) بهطوریکه (فرمول ۲).
فرمول ۱: فرمول ۲:
- ↑ positive integers
- ↑ addition
- ↑ subtraction
- ↑ multiplication
- ↑ division
- ↑ raising to power
- ↑ extraction of roots
- ↑ percentage
- ↑ fractions
- ↑ ratio
- ↑ Babylon
- ↑ astronomy
- ↑ decimal numeral system
- ↑ Mayas
- ↑ John Napier
- ↑ logarithm
- ↑ slide rule
- ↑ binary system
- ↑ modular arithmetic
- ↑ residue arithmetic
- ↑ clock arithmetic
- ↑ commutative law
- ↑ associative law
- ↑ distributive law
- ↑ identity
